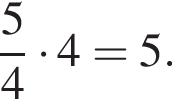Если число а расположено на координатной прямой левее числа b, то зависимость между числами а и b можно записать в виде неравенства:
В треугольнике ABC известно, что 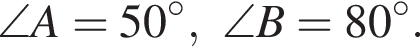 Укажите номер верного утверждения для сторон треугольника.
Укажите номер верного утверждения для сторон треугольника.
Арифметическая прогрессия (an) задана формулой n-го члена an = 3n − 1. Найдите разность этой прогрессии.
Значение выражения 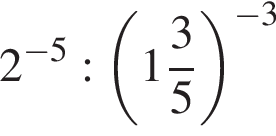 равно:
равно:
Укажите номер выражения, являющегося одночленом восьмой степени:
а) 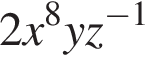 | б) 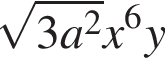 | в) | г) 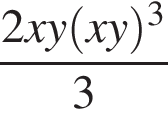 | д) |
На координатной плоскости изображен параллелограмм ABCD с вершинами в узлах сетки (см.рис.). Длина диагонали AC параллелограмма равна:
Длины катетов прямоугольного треугольника являются корнями уравнения x2 − 9x + 12 = 0. Найдите площадь треугольника.
Пусть a = 2,9; b = 8,7 · 103. Найдите произведение ab и запишите его в стандартном виде.
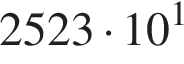
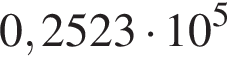
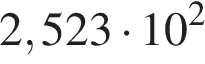
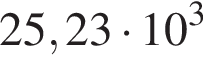
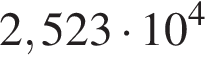
Одна из сторон прямоугольника на 6 см длиннее другой, а его площадь равна 112 см2. Уравнение, одним из корней которого является длина меньшей стороны прямоугольника, имеет вид:
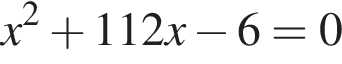
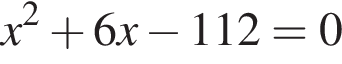
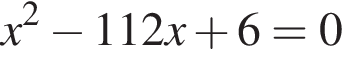
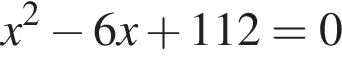
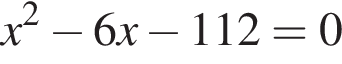
Площадь осевого сечения цилиндра равна 8. Площадь его боковой поверхности равна:
На клетчатой бумаге с клетками размером 1 см х 1 см изображена фигура. Известно, что площадь этой фигуры составляет 32% площади некоторой трапеции. Найдите площадь трапеции в квадратных сантиметрах.
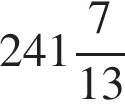 см2
см2Упростите выражение 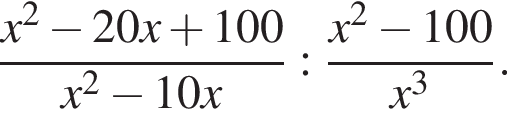
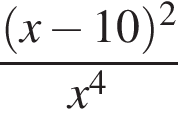
Сократите дробь 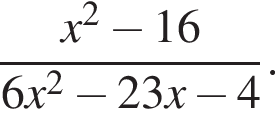
Упростите выражение
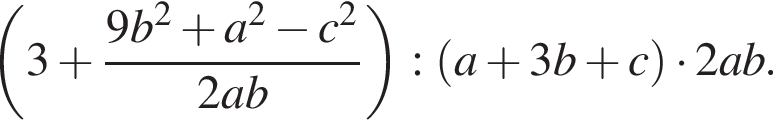
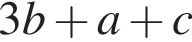
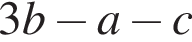
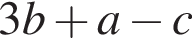
Окружность задана уравнением 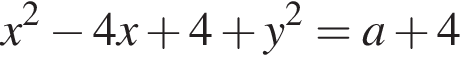 и проходит через вершину параболы
и проходит через вершину параболы 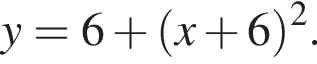 Найдите радиус этой окружности.
Найдите радиус этой окружности.
В ромб площадью ![]() вписан круг площадью 7π. Сторона ромба равна:
вписан круг площадью 7π. Сторона ромба равна:
Через вершину A прямоугольного треугольника ABC (∠C = 90°) проведен перпендикуляр AK к его плоскости. Найдите расстояние от точки K до прямой BC, если AK = 2, AB = 6, BC = ![]()
Корень уравнения
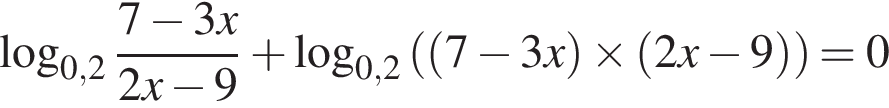
(или сумма корней, если их несколько) принадлежит промежутку:
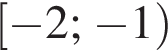
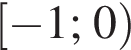
Если в правильной четырехугольной пирамиде высота равна 6, а площадь диагонального сечения равна 9, то ее объем равен ...
Найдите сумму корней (корень, если он единственный) уравнения 
В двух сосудах 38 литров жидкости. Если 5% жидкости из первого сосуда перелить во второй, то в обоих сосудах окажется одинаковое количество жидкости. Сколько литров жидкости было во втором сосуде первоначально?
Найдите сумму наименьшего и наибольшего целых решений неравенства 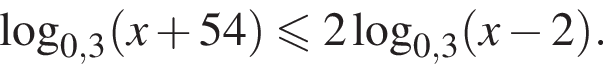
Найдите сумму корней (корень, если он единственный) уравнения 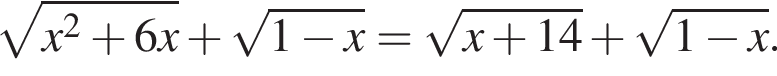
Три числа составляют геометрическую прогрессию, в которой ![]() Если второй член прогрессии уменьшить на 18, то полученные три числа в том же порядке опять составят геометрическую прогрессию. Если третий член новой прогрессии уменьшить на 48, то полученные числа составят арифметическую прогрессию. Найдите сумму исходных чисел.
Если второй член прогрессии уменьшить на 18, то полученные три числа в том же порядке опять составят геометрическую прогрессию. Если третий член новой прогрессии уменьшить на 48, то полученные числа составят арифметическую прогрессию. Найдите сумму исходных чисел.
Четырёхугольник ABCD вписан в окружность. Если 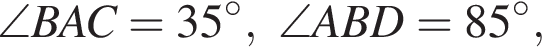 то градусная мера между прямыми AB и CD равна ...
то градусная мера между прямыми AB и CD равна ...
Найдите сумму корней уравнения
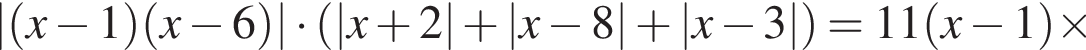
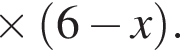
Найдите увеличенную в 3 раза сумму квадратов корней уравнения 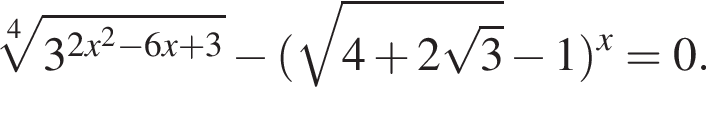
Найдите сумму всех целых чисел из области определения функции 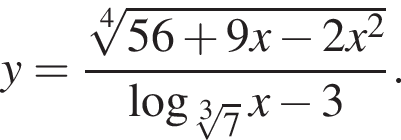
Из двух растворов с различным процентным содержанием спирта массой 200 г и 300 г отлили по одинаковому количеству раствора. Каждый из отлитых растворов долили в остаток другого раствора, после чего процентное содержание спирта в обоих растворах стало одинаковым. Найдите, сколько раствора (в граммах) было отлито из каждого раствора.
Трое рабочих (не все одинаковой квалификации) выполнили некоторую работу, работая поочередно. Сначала первый из них проработал ![]() часть времени, необходимого двум другим для выполнения всей работы. Затем второй проработал
часть времени, необходимого двум другим для выполнения всей работы. Затем второй проработал ![]() часть времени, необходимого двум другим для выполнения всей работы. И, наконец, третий проработал
часть времени, необходимого двум другим для выполнения всей работы. И, наконец, третий проработал ![]() часть времени, необходимого двум другим для выполнения всей работы. Во сколько раз быстрее работа была бы выполнена, если бы трое рабочих работали одновременно? В ответ запишите найденное число, умноженное на 4.
часть времени, необходимого двум другим для выполнения всей работы. Во сколько раз быстрее работа была бы выполнена, если бы трое рабочих работали одновременно? В ответ запишите найденное число, умноженное на 4.

 Значит,
Значит,  — равнобедренный, а стороны AB и BC равны. Поскольку в треугольнике напротив большего угла лежит большая сторона, заключим, что
— равнобедренный, а стороны AB и BC равны. Поскольку в треугольнике напротив большего угла лежит большая сторона, заключим, что  и
и 
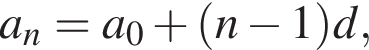 где d — разность арифметической прогрессии. Коэффициент перед n и есть разность арифметической прогрессии, он равен 3.
где d — разность арифметической прогрессии. Коэффициент перед n и есть разность арифметической прогрессии, он равен 3.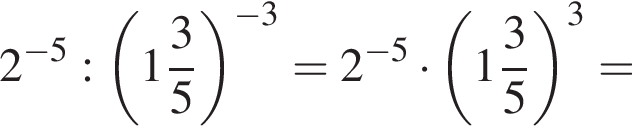
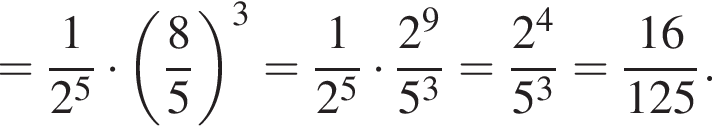
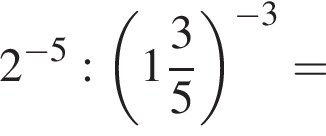
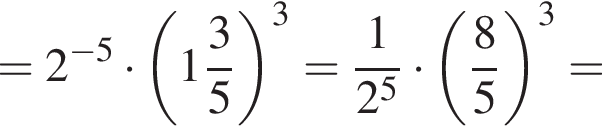
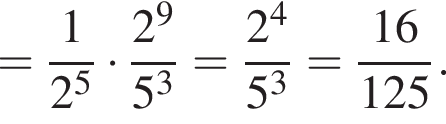
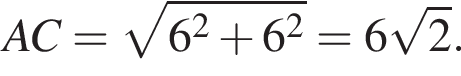
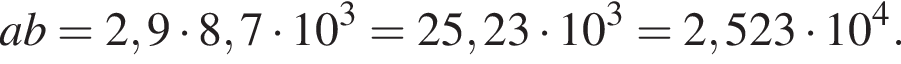
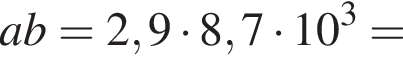
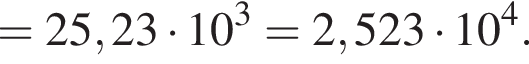
 Тогда получаем:
Тогда получаем: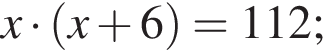
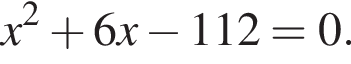
 так как это прямоугольник. Тогда для площади боковой поверхности имеем:
так как это прямоугольник. Тогда для площади боковой поверхности имеем:
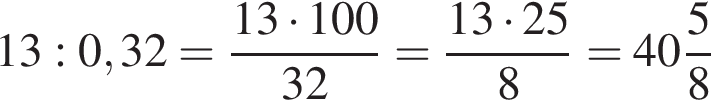 см2.
см2.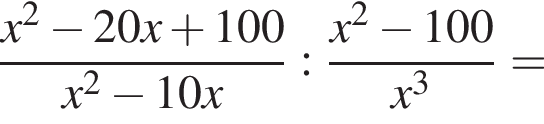
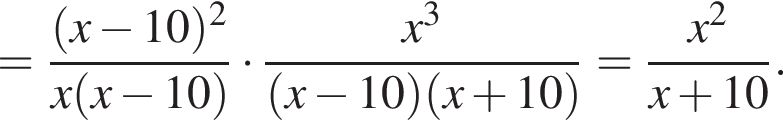
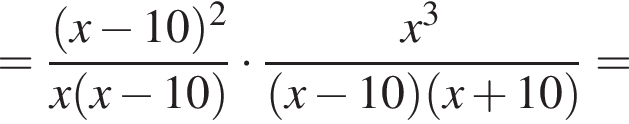
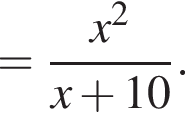
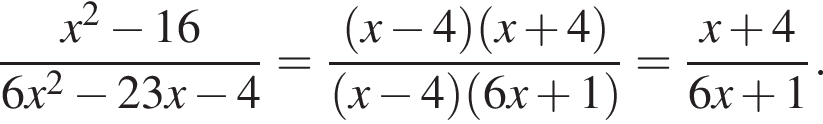
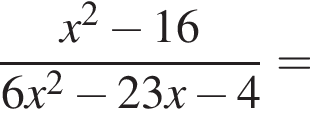
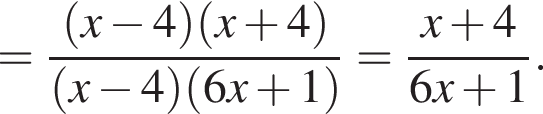
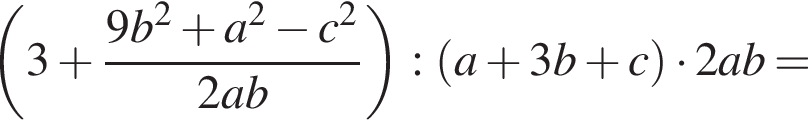
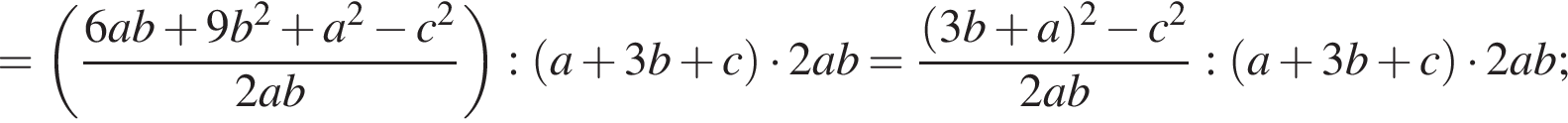
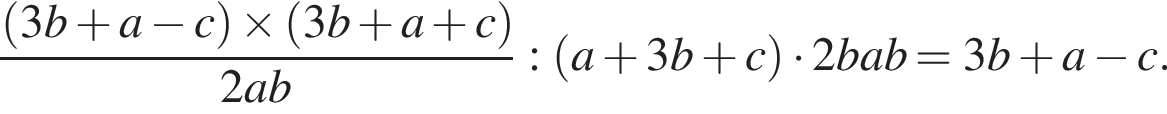
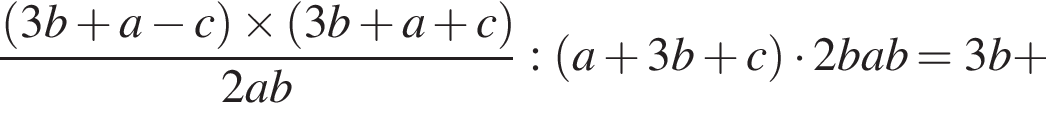
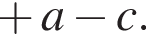
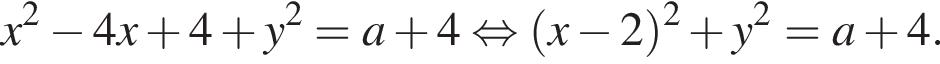
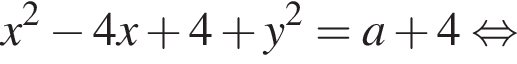

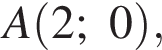 а радиус — это расстояние от точки A до вершины параболы.
а радиус — это расстояние от точки A до вершины параболы.
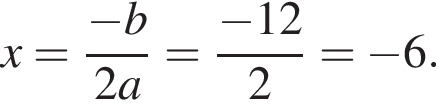 Подставим найденное значение x в изначальное уравнение параболы и получим
Подставим найденное значение x в изначальное уравнение параболы и получим 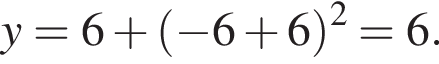 Таким образом, вершина параболы расположена в точке (−6; 6).
Таким образом, вершина параболы расположена в точке (−6; 6).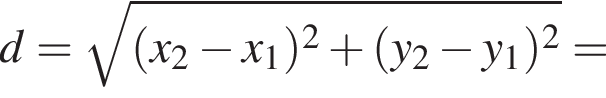
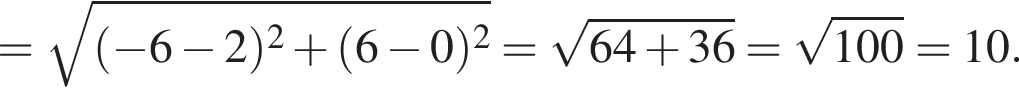
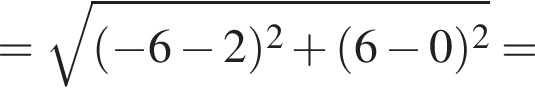

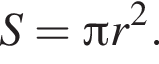 Следовательно, радиус круга равен:
Следовательно, радиус круга равен: 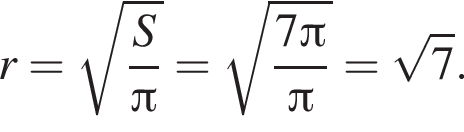 Площадь ромба равна произведению высоты на его сторону:
Площадь ромба равна произведению высоты на его сторону:  Тогда:
Тогда: 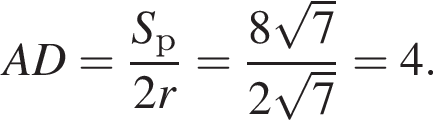
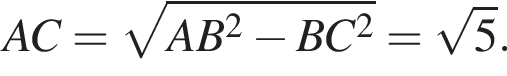 Заметим, что AC является проекцией наклонной KC на плоскость ABC и AC
Заметим, что AC является проекцией наклонной KC на плоскость ABC и AC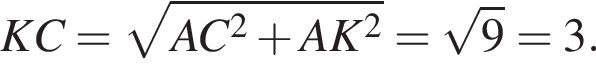
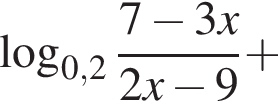

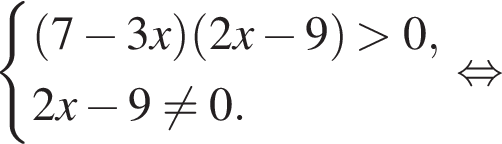
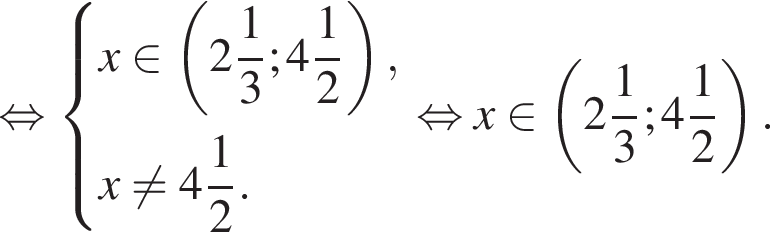
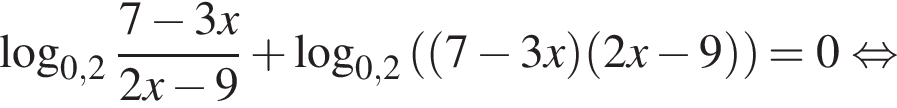
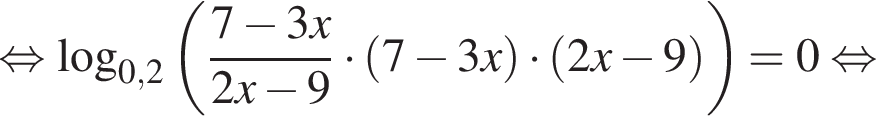
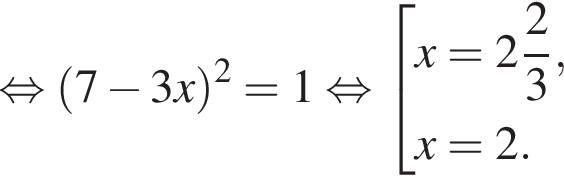
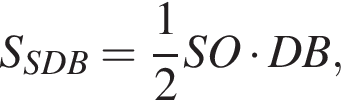 следовательно,
следовательно, 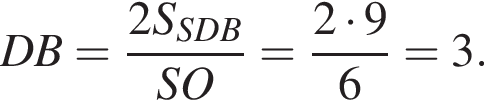
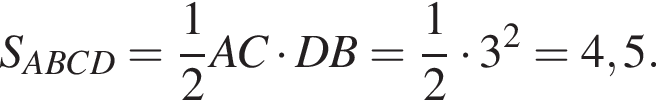 Следовательно,
Следовательно,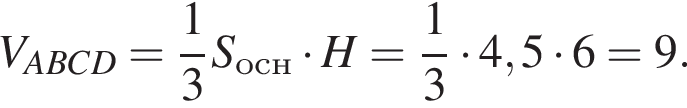
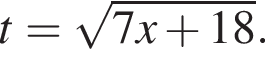 Тогда:
Тогда: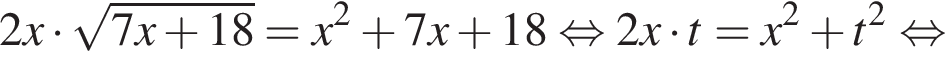

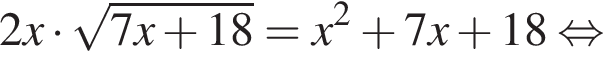


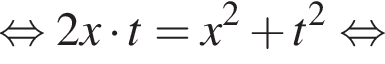
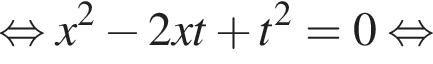
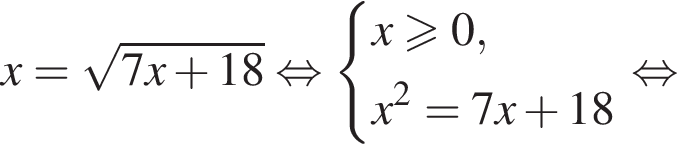
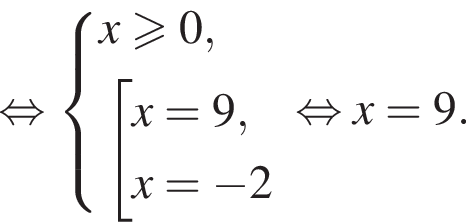
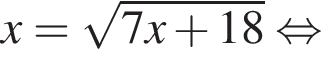
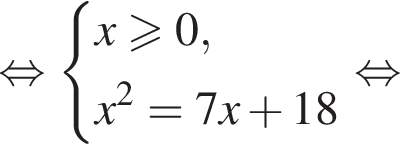
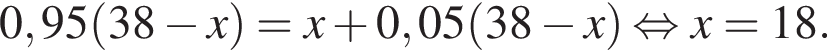
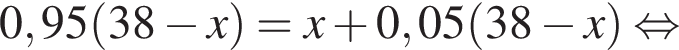

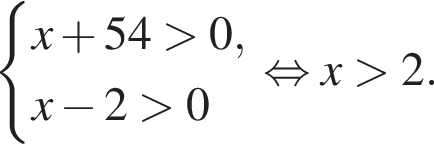
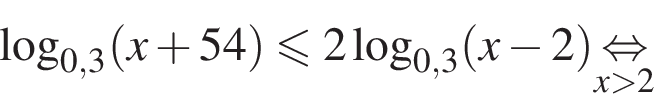
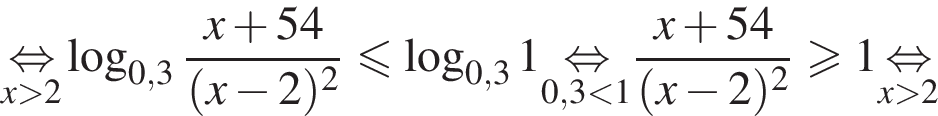
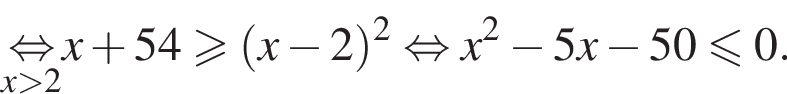
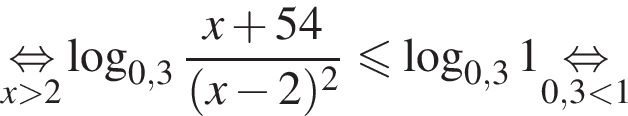
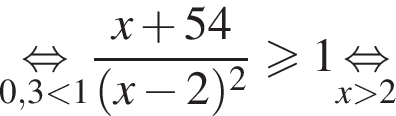

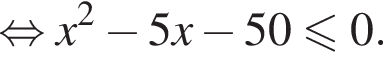
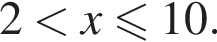 Наименьшим целым решением неравенства является число 3, наибольшим целым решением — число 10, их сумма равна 13.
Наименьшим целым решением неравенства является число 3, наибольшим целым решением — число 10, их сумма равна 13.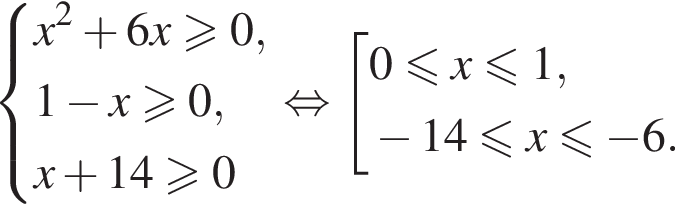
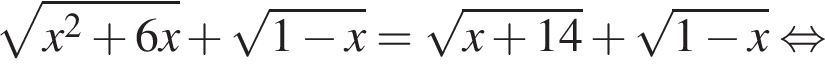
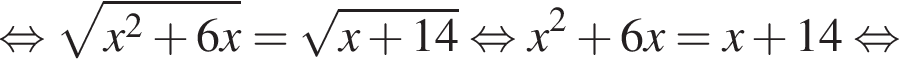
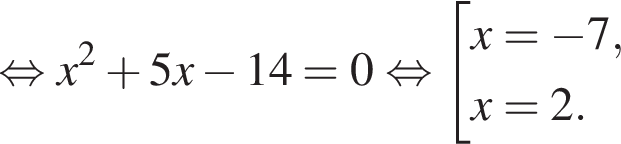
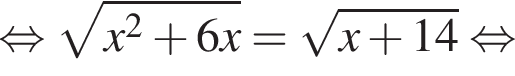
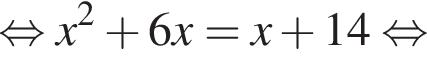
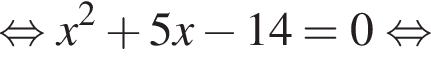
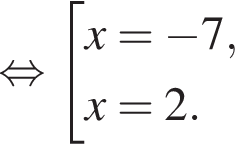
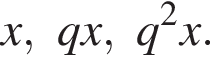
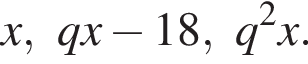
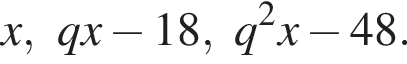
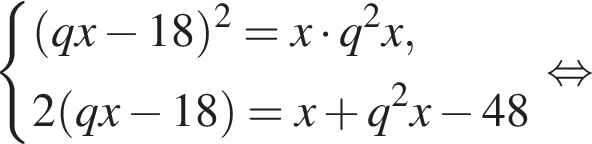
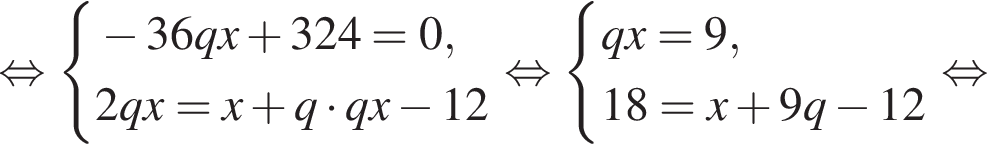
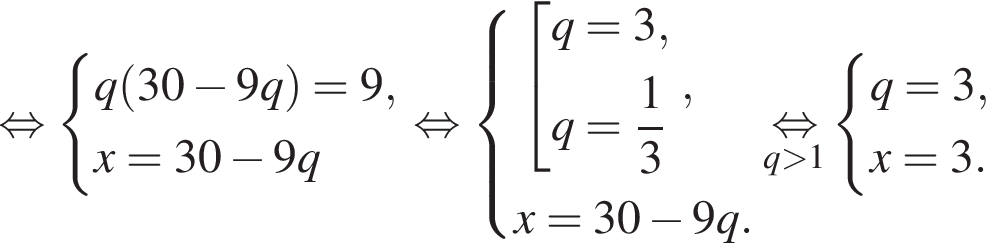
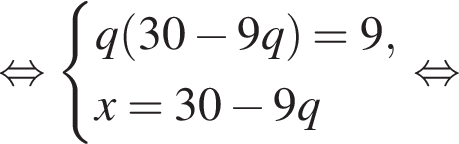
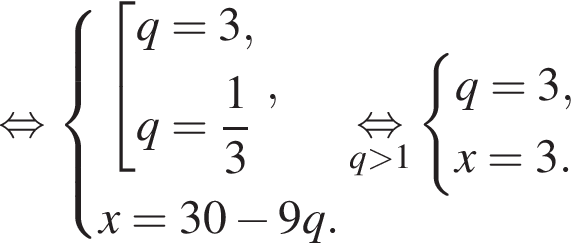
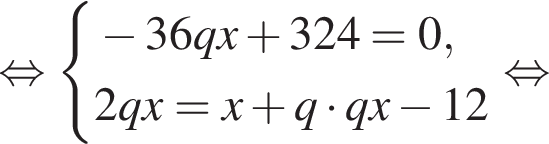
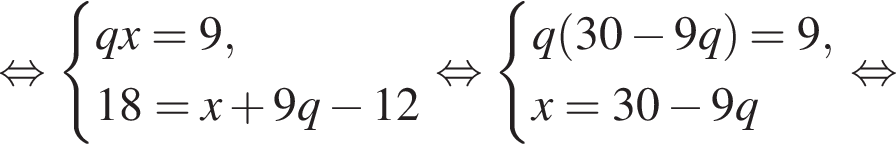
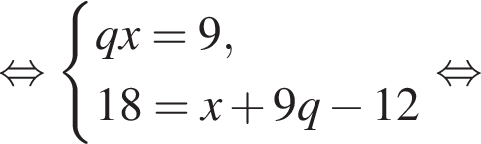





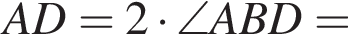
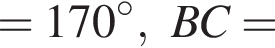
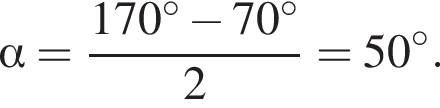

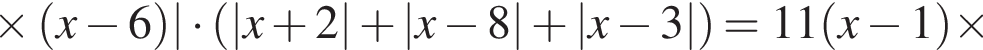
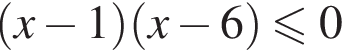 :
: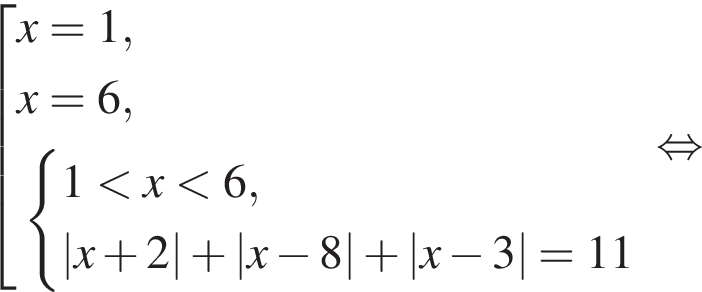
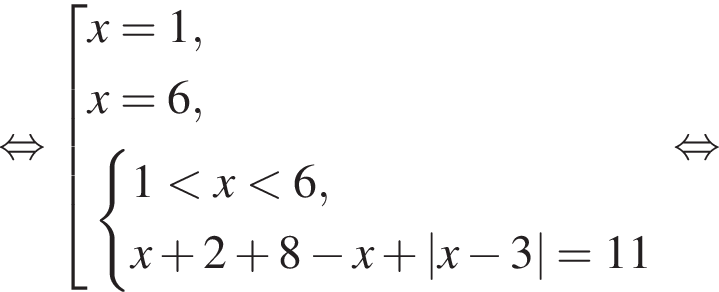
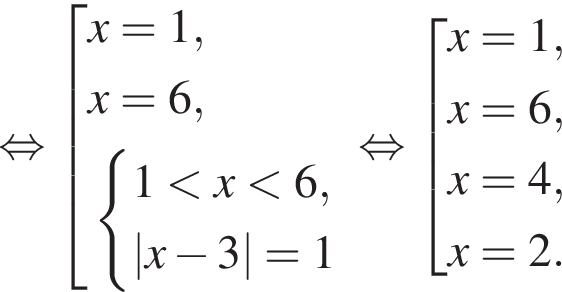
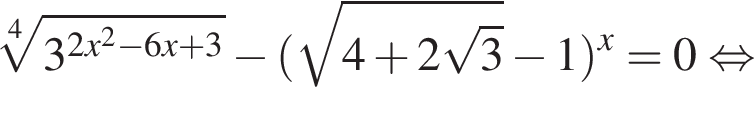
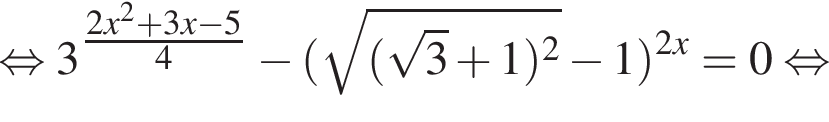
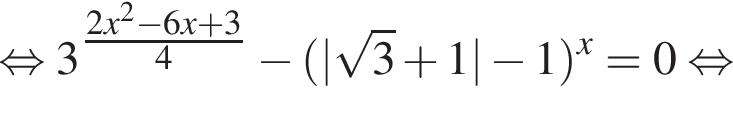
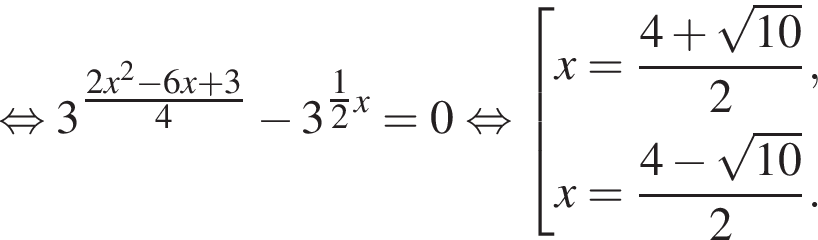
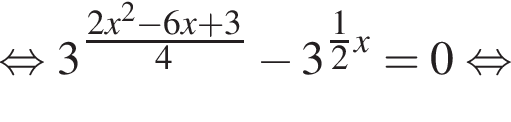
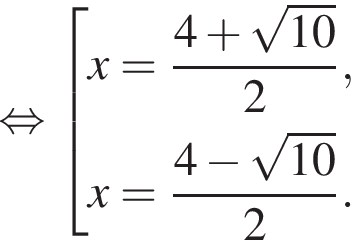
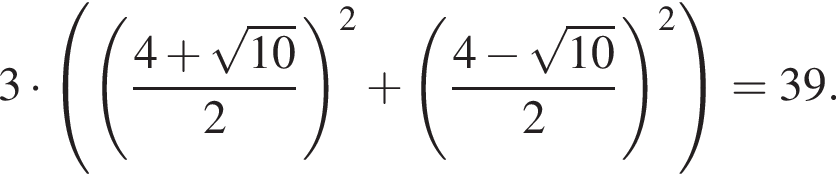
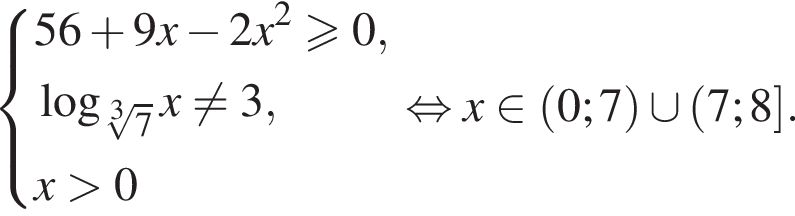
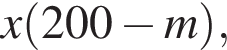 во втором —
во втором — 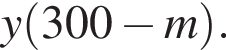 После переливания масса спирта в 1-ом сосуде равна
После переливания масса спирта в 1-ом сосуде равна 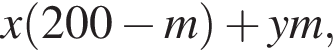 во втором —
во втором —  Так как концентрации стали одинаковыми, а объёмы относятся как 2:3, во втором сосуде в 1,5 раза больше спирта. Тогда:
Так как концентрации стали одинаковыми, а объёмы относятся как 2:3, во втором сосуде в 1,5 раза больше спирта. Тогда:


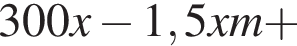
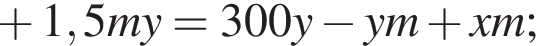
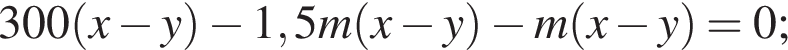

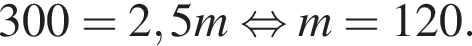
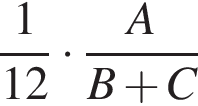 работы.
работы. 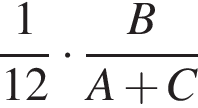 работы.
работы. 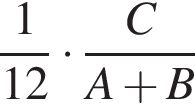 работы.
работы. 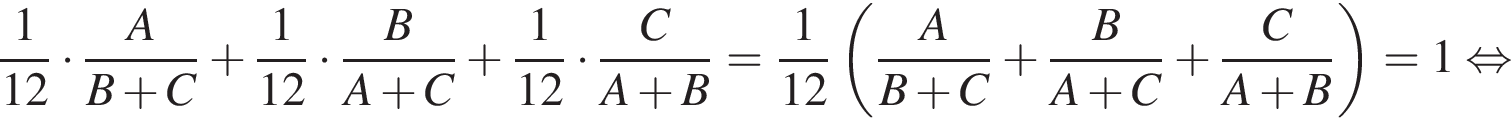
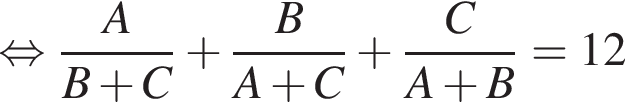
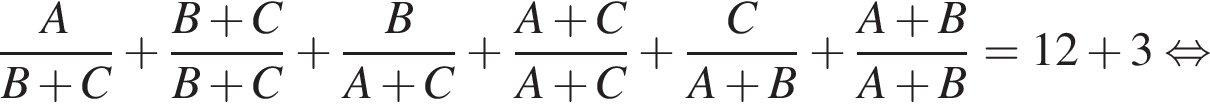
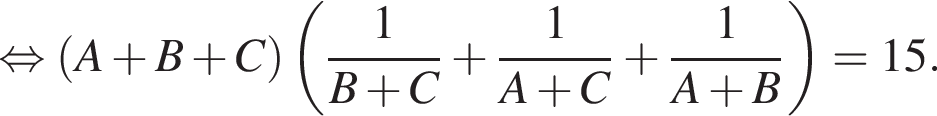
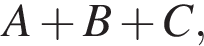 то они выполнили бы работу за:
то они выполнили бы работу за: 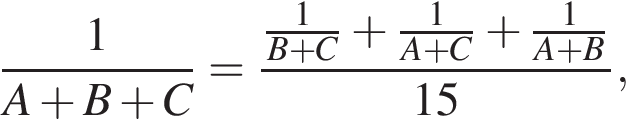
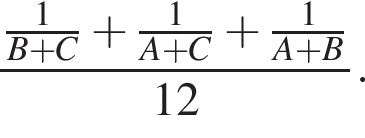 Поэтому, работая вместе работа была бы выполнена в
Поэтому, работая вместе работа была бы выполнена в 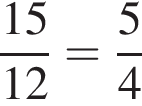 раза быстрее. В ответе будет число
раза быстрее. В ответе будет число